何小鹏谈DeepSearch,引领深度搜索未来趋势
何小鹏关于DeepSearch的见解引领深度搜索未来发展方向。他强调,随着数据量的增长,深度搜索需不断创新,以满足用户对精准、个性化搜索的需求。何小鹏认为,DeepSearch将更加注重智能算法的应用,提升搜索结果的...
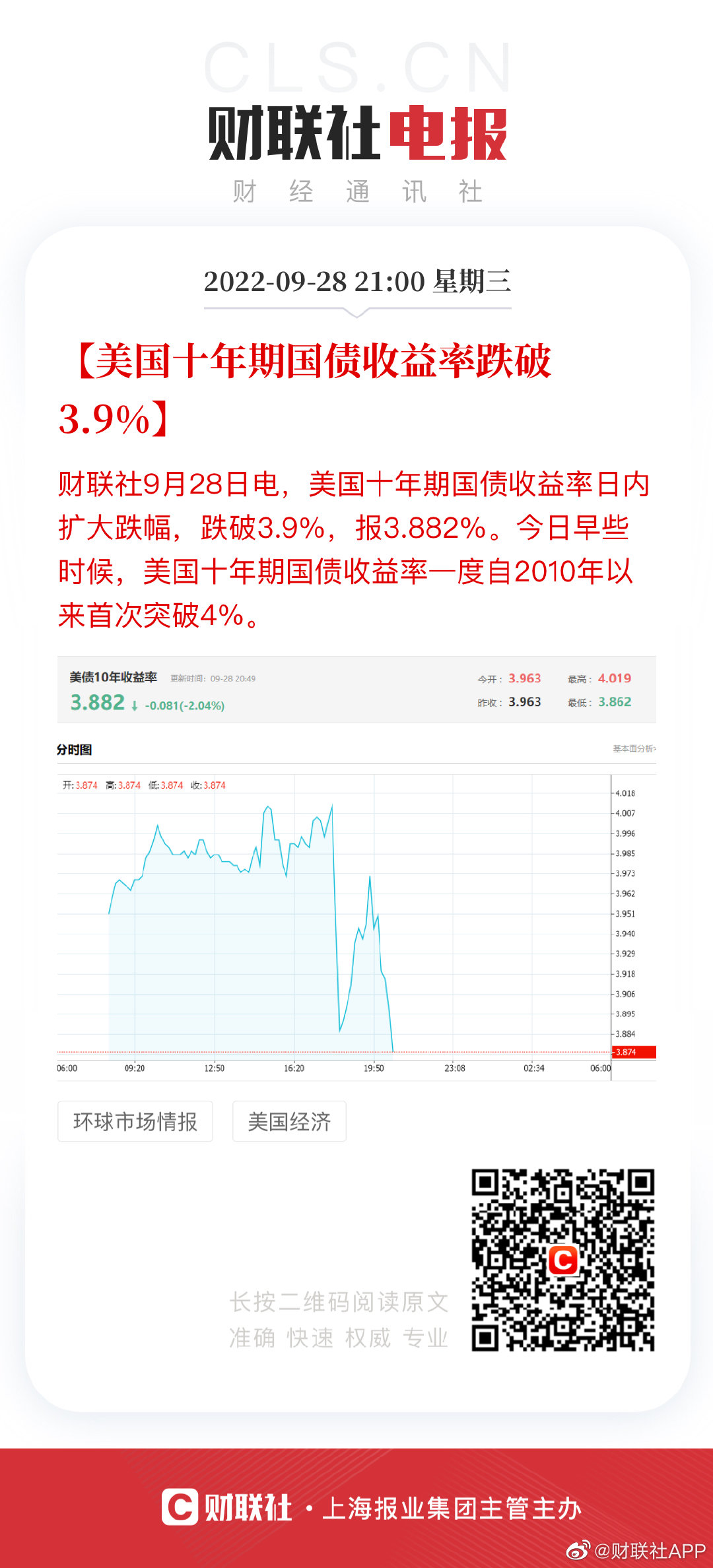
美债收益率跌至年内低点,影响、原因与未来展望分析
美债收益率跌至年内低点,对全球金融市场产生了广泛影响。这一现象主要受到美联储持续加息、全球经济形势不确定性以及投资者风险偏好下降等多重因素的影响。随着美联储政策调整、全球经济复苏进程以及市场情绪的演变,美债收益率的走...
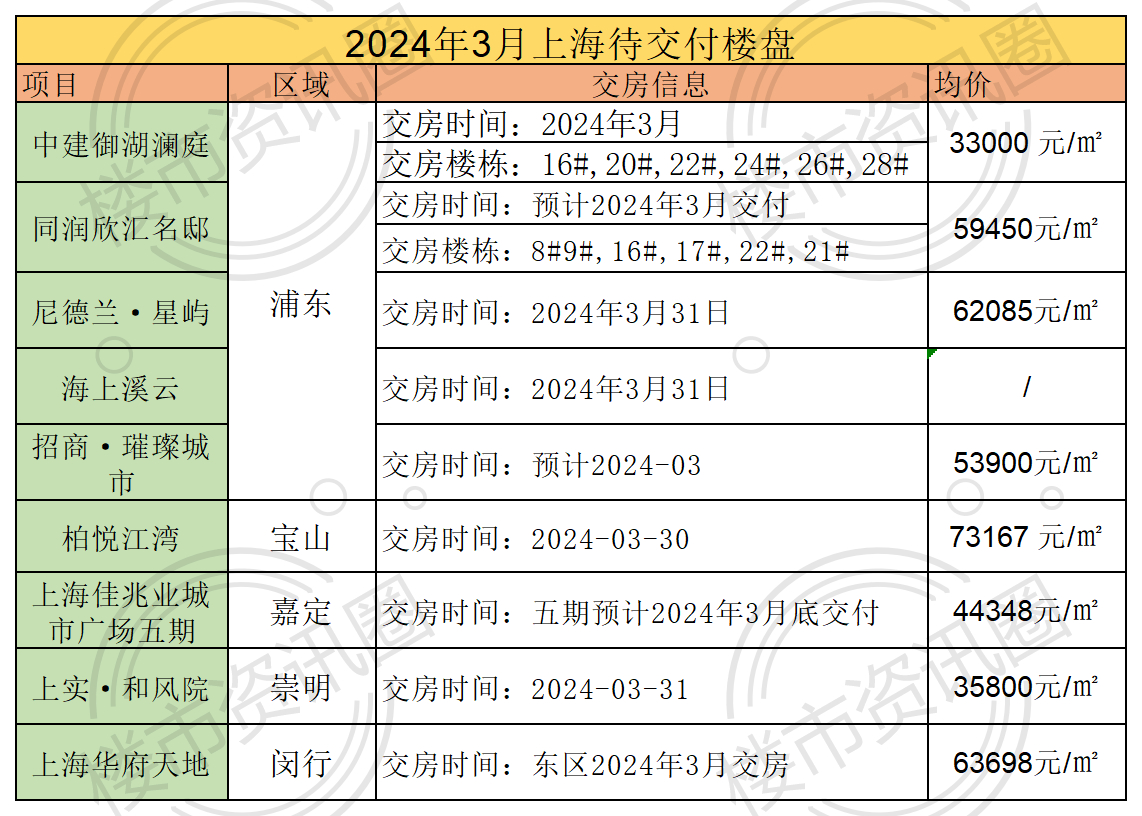
上海新房交付热潮来袭,87个项目交付的市场展望与影响分析
上海即将迎来新房交付热潮,共有87个项目即将交付使用。这一趋势将对市场产生重要影响,有望带动周边地区的发展,提高居民生活质量。这也将为购房者提供更多选择,促进市场竞争的加剧。交付的新房项目将带来投资回报的机遇,也将对...
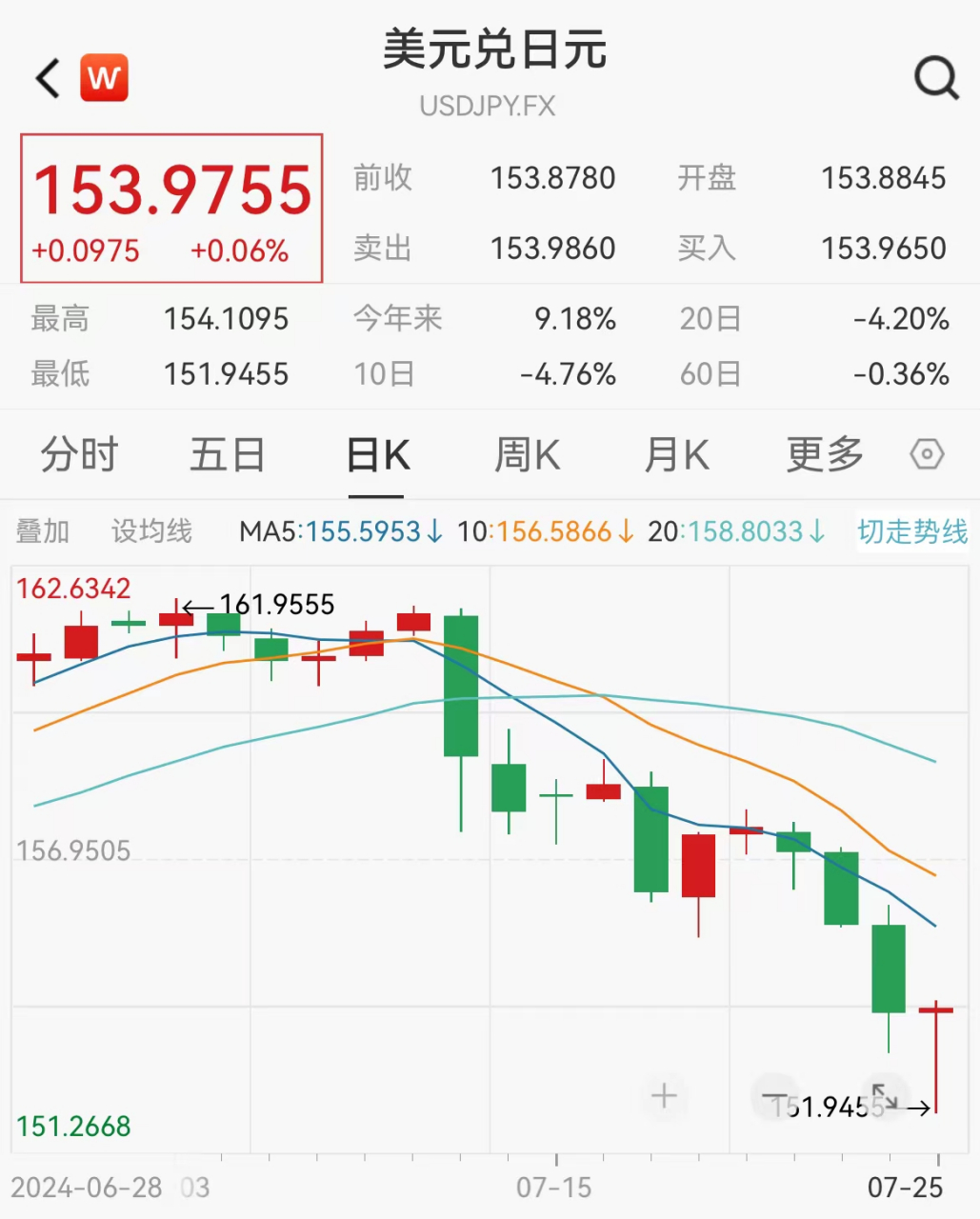
日元兑美元突破152关口,货币走势背后的动因及影响深度解析
摘要:近期日元兑美元汇率突破152关口,引起市场关注。货币走势背后的因素包括全球经济形势、货币政策差异、贸易关系等。日元升值对日本出口企业带来压力,但可能有利于进口企业和投资者。全球货币汇率波动对国际贸易和投资产生广...
松下放弃电视机业务,转型路径及未来展望
松下公司正式宣布放弃电视机业务,将进行业务转型。这一决策标志着该公司将调整战略重心,寻求新的发展道路。未来松下将更注重技术创新和转型升级,以应对市场变化和消费者需求的变化。虽然放弃电视机业务是一个重大决策,但松下对未...
万科新任办公室副主任万梅,角色展望与企业文化深度解读的洞察
万科任命万梅为新任办公室副主任,这一人事变动备受关注。万梅的任命不仅代表着公司对其能力的认可,也预示着她在未来角色中将发挥重要作用。作为新任办公室副主任,万梅将承担起协调内外、推动企业文化建设等重要职责。其个人风格与...
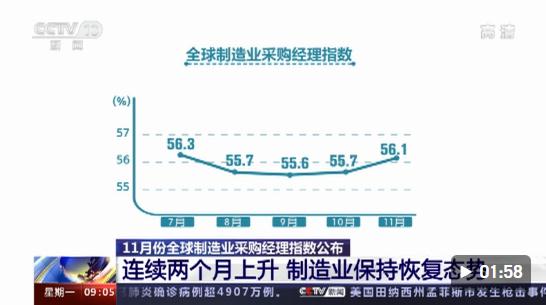
全球制造业PMI揭示发展趋势与挑战,行业洞察与前景展望
全球制造业PMI公布,反映了制造业的最新发展趋势和挑战。数据显示,制造业在扩张与收缩之间徘徊,面临需求增长放缓、成本压力上升等挑战。新技术应用、产业升级等因素为制造业带来机遇。企业需要灵活应对市场变化,寻求创新和发展...
万科重整启新篇,工作组进驻引领企业变革之路
万科重整,工作组进驻,标志着这家企业开启了新的篇章。工作组的到来为企业带来了新的机遇与挑战,将助力万科优化资源配置、提升运营效率,并寻求新的发展机会。此举旨在推动万科实现可持续发展,并进一步提升其在行业内的竞争力。预...
华为未来展望,销售收入预计超8600亿的战略前瞻与未来发展
华为预计至2024年销售收入将超过8600亿元人民币,展现出强大的战略前瞻和未来展望。该公司将继续致力于技术研发和创新,推动数字化转型和智能化发展,助力全球信息社会的繁荣与进步。华为的战略布局着眼于长期发展,注重技术...
雅马哈股价飙升背后的原因及市场展望,上涨9.5%的趋势分析
雅马哈股价近期飙升,涨幅高达9.5%。其股价上涨的原因可能与公司业绩增长、市场前景广阔等因素有关。投资者对于雅马哈未来的市场表现也持有乐观态度。市场展望方面,雅马哈在相关领域的持续创新和良好口碑有望推动其股价继续上涨...









 京ICP备13041877号
京ICP备13041877号